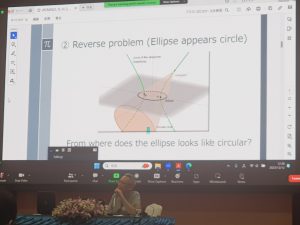
12月12日、タイのパタヤで招待講演を行いました。数学とテクノロジーに関する国際会議ATCM2023(Asian Technology Conference in Mathematics)で、タイトルは「Locus of viewpoints from which a conic appears circular」(二次曲線が円に見える視点の軌跡)です。内容は中高生にもわかる初等的な数学です。円を地面に置いて様々な視点から見ると、円が楕円に見えることは皆さんもご存じでしょう。では、楕円を地上に置いてみるとどうでしょう?楕円を地面に置いて様々な視点から見ると、楕円が円に見える視点がたくさんあり、楕円が円に見える視点全体は双曲線になります。逆に、双曲線を地面に置いて様々な視点から見ると、双曲線が円(の一部)に見える視点全体は楕円になります。放物線を地面に置いたらどうなるのでしょう?このように、身近なところに数学は潜んでおり、美しい双対性を見出すことができます。QRコードを読み取ると、発表で用いた資料を見ることができます。その中に三角関数に関する問題とその答えがあるので、腕に覚えのある人は是非チャレンジしてみて下さい。この問題は球面上の楕円から導かれるもので、そこにも双対性が潜んでいます。資料の最後の方にある写真は、水平線が私たちに自分が立っている標高を教えてくれている、というものです(水平線と山の稜線との交点に注目して下さい)。(文章:前田陽一)